Writing your own recipe

Overview

Teaching: 15 min
Exercises: 30 min
Compatibility: ESMValTool v2.6.0

Questions

How do I create a new recipe?

Can I use different preprocessors for different variables?

Can I use different datasets for different variables?

How can I combine different preprocessor functions?

Objectives

Create a recipe with multiple preprocessors

Use different preprocessors for different variables

Run a recipe with variables from different datasets

Introduction

One of the key strenghts of ESMValTool is in making complex analyses reusable and reproducible. But that doesn’t mean everything in ESMValTool needs to be complex. Sometimes, the biggest challenge is in keeping things simple. You probably know the ‘warming stripes’ visualization by Professor Ed Hawkins. On the site https://showyourstripes.info you can find the same visualization for many regions in the world.

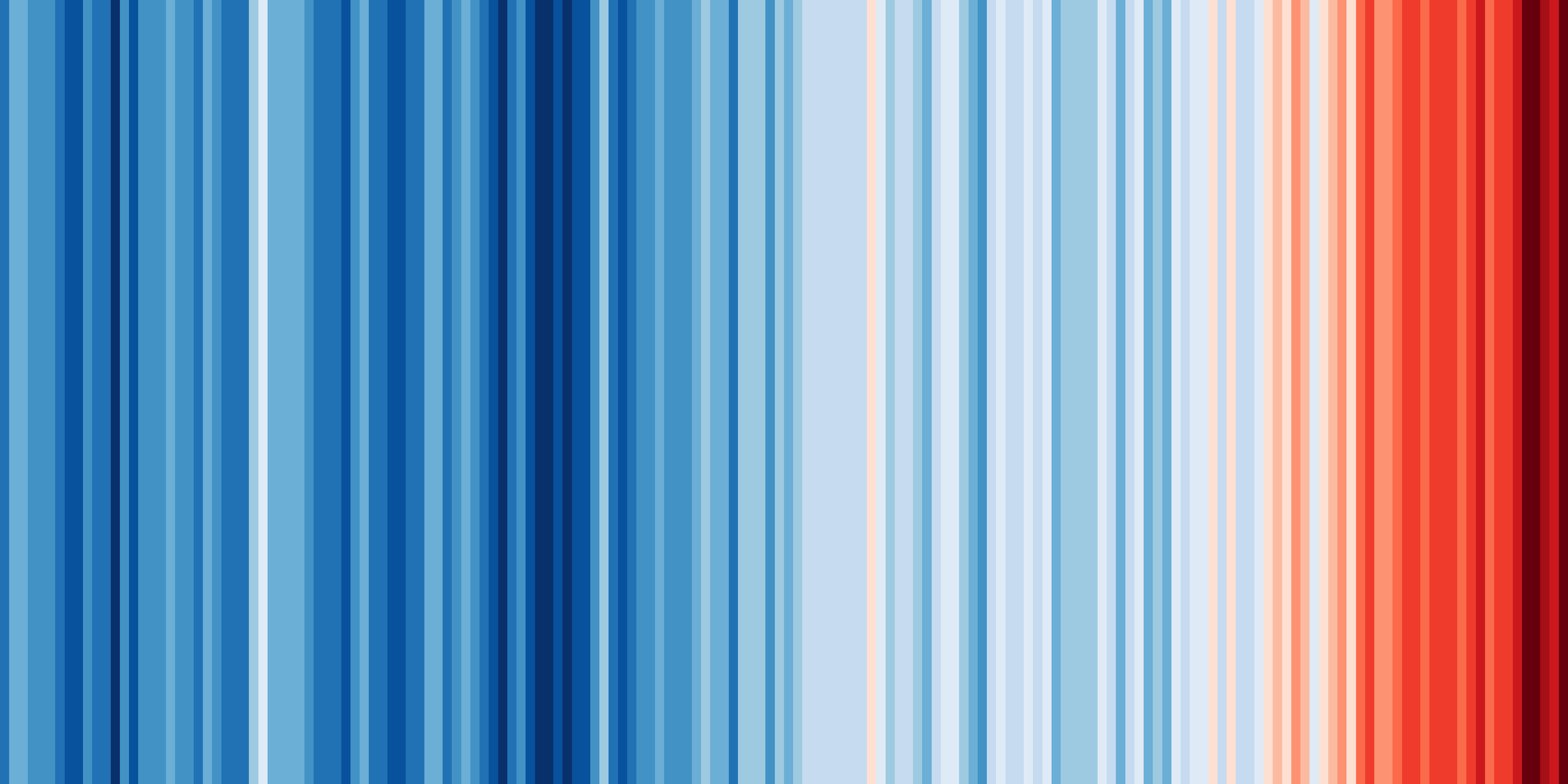Warming stripes Shared by Ed Hawkins under a Creative Commons 4.0 Attribution International licence. Source: https://showyourstripes.info

In this episode, we will reproduce and extend this functionality with ESMValTool. We have prepared a small Python script that takes a NetCDF file with timeseries data, and visualizes it in the form of our desired warming stripes figure.

You can find the diagnostic script that we will use here (warming_stripes.py).

Download the file and store it in your working directory. If you want, you may also have a look at the contents, but it is not necessary to follow along.

We will write an ESMValTool recipe that takes some data, performs the necessary preprocessing, and then runs our Python script.

Drawing up a plan

Previously, we saw that running ESMValTool executes a number of tasks. Write down what tasks we will need to execute in this episode and what each of these tasks does?

Answer

In this episode, we will need to do 2 tasks:

A preprocessing task that converts the gridded temperature data to a timeseries of global temperature anomalies

A diagnostic tasks that calls our Python script, taking our preprocessed timeseries data as input.

Building a recipe from scratch

The easiest way to make a new recipe is to start from an existing one, and modify it until it does exactly what you need. However, in this episode we will start from scratch. This forces us to think about all the steps. We will deal with common errors as they occur throughout the development.

Remember the basic structure of a recipe, and notice that each of them is extensively described in the documentation under the header “The recipe format”:

This is the first place to look for help if you get stuck.

Open a new file called recipe_warming_stripes.yml:

nano recipe_warming_stripes.yml

Let’s add the standard header comments (these do not do anything), and a first description.

# ESMValTool
# recipe_warming_stripes.yml
---
documentation:
  description: Reproducing Ed Hawkins' warming stripes visualization
  title: Reproducing Ed Hawkins' warming stripes visualization.

Notice that yaml always requires 2 spaces indentation between the different levels. Pressing ctrl+o will save the file. Verify the filename at the bottom and press enter. Then use ctrl+x to exit the editor.

We will try to run the recipe after every modification we make, to see if it (still) works.

esmvaltool run recipe_warming_stripes.yml

In this case, it gives an error. Below you see the last few lines of the error message.

...
Error validating data /home/user/esmvaltool_tutorial/recipe_warming_stripes.yml
        with schema /home/user/mambaforge/envs/esmvaltool_tutorial/lib/python3.10
        /site-packages/esmvalcore/recipe_schema.yml
            documentation.authors: Required field missing
YYYY-MM-DD HH:mm:SS,NNN UTC [19451] INFO    If you have a question or need help,
    please start a new discussion on https://github.com/ESMValGroup/
    ESMValTool/discussions
If you suspect this is a bug, please open an issue on
    https://github.com/ESMValGroup/ESMValTool/issues
To make it easier to find out what the problem is, please consider attaching
    the files run/recipe_*.yml and run/main_log_debug.txt from the output directory.

Here, ESMValTool is telling us that it is missing a required field, namely the authors. We see that ESMValTool always tries to validate the recipe at an early stage.

Let’s add some additional information to the recipe. Open the recipe file again, and add an authors section below the description. ESMValTool expects the authors as a list, like so:

authors:
  - lastname_firstname

To bypass a number of similar error messages, add a minimal diagnostics section below the documentation. The file should now look like:

# ESMValTool
# recipe_warming_stripes.yml
---
documentation:
  description: Reproducing Ed Hawkins' warming stripes visualization
  title: Reproducing Ed Hawkins' warming stripes visualization.

  authors:
    - doe_john
diagnostics:
  dummy_diagnostic_1:
    scripts: null

This is the minimal recipe layout that is required by ESMValTool. If we now run the recipe again, you will probably see the following error:

ValueError: Tag 'doe_john' does not exist in section 'authors' of 
	    /home/user/mambaforge/envs/esmvaltool_tutorial/python3.10/
	    site-packages/esmvaltool/config-references.yml

Pro tip: config-references.yml

The error message above points to a file named config-references.yml. This is where ESMValTool stores all its citation information. To add yourself as an author, add your name in the form lastname_firstname in alphabetical order following the existing entries, under the # Development team comment. See the List of authors section in the ESMValTool documentation for more information.

For now, let’s just use one of the existing references. Change the author field to righi_mattia, who cannot receive enough credit for all the effort he put into ESMValTool. If you now run the recipe again, you should see the final message

ERROR   No tasks to run!

Although there is no actual error in the recipe, ESMValTool assumes you mistakenly left out a variable name to process and alerts you with this error message.

Adding a dataset entry

Let’s add a datasets section. We will reuse the same datasets that we used in previous episodes.

Filling in the dataset keys

Use the paths specified in the configuration file to explore the data directory, and look at the explanation of the dataset entry in the ESMValTool documentation. For both the datasets, write down the following properties:

project

variable (short name)

CMIP table

dataset (model name or obs/reanalysis dataset)

experiment

ensemble member

grid

start year

end year

Answers

key file 1 file 2

project CMIP6 CMIP5

short name tas tas

CMIP table Amon Amon

dataset BCC-ESM1 CanESM2

experiment historical historical

ensemble r1i1p1f1 r1i1p1

grid gn (native grid) N/A

start year 1850 1850

end year 2014 2005

Note that the grid key is only required for CMIP6 data, and that the extent of the historical period has changed between CMIP5 and CMIP6.

We start with the BCC-ESM1 dataset and add a datasets section to the recipe, listing a single dataset, as shown below. Note that key fields such as mip or start_year are included in the datasets section here but are part of the diagnostic section in the recipe example seen in Running your first recipe.

datasets:
  - {dataset: BCC-ESM1, project: CMIP6, mip: Amon, exp: historical, 
     ensemble: r1i1p1f1, grid: gn, start_year: 1850, end_year: 2014}

The recipe should run but produce the same message as in the previous case since we still have not included a variable to actually process. We have not included the short name of the variable in this dataset section because this allows us to reuse this dataset entry with different variable names later on. This is not really necessary for our simple use case, but it is common practice in ESMValTool.

Adding the preprocessor section

Above, we already described the preprocessing task that needs to convert the standard, gridded temperature data to a timeseries of temperature anomalies.

Defining the preprocessor

Have a look at the available preprocessors in the documentation. Write down

Which preprocessor functions do you think we should use?

What are the parameters that we can pass to these functions?

What do you think should be the order of the preprocessors?

A suitable name for the overall preprocessor

Solution

We need to calculate anomalies and global means. There is an anomalies preprocessor which needs a granularity, a reference period, and whether or not to standardize the data. The global means can be calculated with the area_statistics preprocessor, which takes an operator as argument (in our case we want to compute the mean).

The default order in which these preprocessors are applied can be seen here: area_statistics comes before anomalies. If you want to change this, you can use the custom_order preprocessor. We will keep it like this.

Let’s name our preprocessor global_anomalies.

Add the following block to your recipe file:

preprocessors:
  global_anomalies:
    area_statistics:
      operator: mean
    anomalies:
        period: month
        reference:
          start_year: 1981
          start_month: 1
          start_day: 1
          end_year: 2010
          end_month: 12
          end_day: 31
        standardize: false

Completing the diagnostics section

Now we are ready to finish our diagnostics section. Remember that we want to make two tasks: a preprocessor task, and a diagnostic task. To illustrate that we can also pass settings to the diagnostic script, we add the option to specify a custom colormap.

Fill in the blanks

Extend the diagnostics section in your recipe by filling in the blanks in the following template:

diagnostics:
  <... (suitable name for our diagnostic)>:
    description: <...>
    variables:
      <... (suitable name for the preprocessed variable)>:
        short_name: <...>
        preprocessor: <...>
    scripts:
      <... (suitable name for our python script)>:
        script: <full path to python script>
        colormap: <... choose from matplotlib colormaps>

Solution

diagnostics:
  diagnostic_warming_stripes:
    description: visualize global temperature anomalies as warming stripes
    variables:
      global_temperature_anomalies_global:
        short_name: tas
        preprocessor: global_anomalies
    scripts:
      warming_stripes_script:
        script: ~/esmvaltool_tutorial/warming_stripes.py
        colormap: 'bwr'

Now you should be able to run the recipe to get your own warming stripes.

Note: for the purpose of simplicity in this episode, we have not added logging or provenance tracking in the diagnostic script. Once you start to develop your own diagnostic scripts and want to add them to the ESMValTool repositories, this will be required. However, writing your own diagnostic script is beyond the scope of the basic tutorial.

Bonus exercises

Below are a couple of exercise to practice modifying the recipe. For your reference, here’s a copy of the recipe at this point. This will be the point of departure for each of the modifications we’ll make below.

Specific location

On showyourstripes.org, you can download stripes for specific locations. We will reproduce this possibility. Look at the available preprocessors in the documentation, and replace the global mean with a suitable alternative.
Solution

You could have used extract_point or extract_region. We used extract_point. Here’s a copy of the recipe at this point and this is the difference from the previous recipe:
--- recipe_warming_stripes.yml
+++ recipe_warming_stripes_local.yml
@@ -10,9 +10,11 @@
   - {dataset: BCC-ESM1, project: CMIP6, mip: Amon, exp: historical, 
      ensemble: r1i1p1f1, grid: gn, start_year: 1850, end_year: 2014}

 preprocessors:
-  global_anomalies:
-    area_statistics:
-      operator: mean
+  anomalies_amsterdam:
+    extract_point:
+      latitude: 52.379189
+      longitude: 4.899431
+      scheme: linear
     anomalies:
       period: month
       reference:
@@ -27,9 +29,9 @@
 diagnostics:
   diagnostic_warming_stripes:
     variables:
-      global_temperature_anomalies:
+      temperature_anomalies_amsterdam:
         short_name: tas
-        preprocessor: global_anomalies
+        preprocessor: anomalies_amsterdam
     scripts:
       warming_stripes_script:
         script: ~/esmvaltool_tutorial/warming_stripes.py

Different periods

Split the diagnostic in 2: the second one should use a different period. You’re free to choose the periods yourself. For example, 1 could be ‘recent’, the other ‘20th_century’. For this, you’ll have to add a new variable group.

Solution

Here’s a copy of the recipe at this point and this is the difference with the previous recipe:

--- recipe_warming_stripes_local.yml
+++ recipe_warming_stripes_periods.yml
@@ -7,7 +7,7 @@
     - righi_mattia

 datasets:
-  - {dataset: BCC-ESM1, project: CMIP6, mip: Amon, exp: historical, 
-  	  ensemble: r1i1p1f1, grid: gn, start_year: 1850, end_year: 2014}
+  - {dataset: BCC-ESM1, project: CMIP6, mip: Amon, exp: historical, 
+     ensemble: r1i1p1f1, grid: gn}

 preprocessors:
   anomalies_amsterdam:
@@ -29,9 +29,16 @@
 diagnostics:
   diagnostic_warming_stripes:
     variables:
-      temperature_anomalies_amsterdam:
+      temperature_anomalies_recent:
         short_name: tas
         preprocessor: anomalies_amsterdam
+        start_year: 1950
+        end_year: 2014
+      temperature_anomalies_20th_century:
+        short_name: tas
+        preprocessor: anomalies_amsterdam
+        start_year: 1900
+        end_year: 1999
     scripts:
       warming_stripes_script:
         script: ~/esmvaltool_tutorial/warming_stripes.py

Different preprocessors

Now that you have different variable groups, we can also use different preprocessors. Add a second preprocessor to add another location of your choosing.

Pro-tip: if you want to avoid repetition, you can use YAML anchors.

Solution

Here’s a copy of the recipe at this point and this is the difference with the previous recipe:

--- recipe_warming_stripes_periods.yml
+++ recipe_warming_stripes_multiple_locations.yml
@@ -15,7 +15,7 @@
       latitude: 52.379189
       longitude: 4.899431
       scheme: linear
-    anomalies:
+    anomalies: &anomalies
       period: month
       reference:
         start_year: 1981
@@ -25,18 +25,24 @@
         end_month: 12
         end_day: 31
       standardize: false
+  anomalies_london:
+    extract_point:
+      latitude: 51.5074
+      longitude: 0.1278
+      scheme: linear
+    anomalies: *anomalies

 diagnostics:
   diagnostic_warming_stripes:
     variables:
-      temperature_anomalies_recent:
+      temperature_anomalies_recent_amsterdam:
         short_name: tas
         preprocessor: anomalies_amsterdam
         start_year: 1950
         end_year: 2014
-      temperature_anomalies_20th_century:
+      temperature_anomalies_20th_century_london:
         short_name: tas
-        preprocessor: anomalies_amsterdam
+        preprocessor: anomalies_london
         start_year: 1900
         end_year: 1999
     scripts:

Additional datasets

So far we have defined the datasets in the datasets section of the recipe. However, it’s also possible to add specific datasets only for specific variable groups. Look at the documentation to learn about the ‘additional_datasets’ keyword, and add a second dataset only for one of the variable groups.
Solution

Here’s a copy of the recipe at this point and this is the difference with the previous recipe:
--- recipe_warming_stripes_multiple_locations.yml
+++ recipe_warming_stripes_additional_datasets.yml
@@ -45,6 +45,8 @@
         preprocessor: anomalies_london
         start_year: 1900
         end_year: 1999
+        additional_datasets:
+          - {dataset: CanESM2, project: CMIP5, mip: Amon, exp: historical, ensemble: r1i1p1}
     scripts:
       warming_stripes_script:
         script: ~/esmvaltool_tutorial/warming_stripes.py

Key Points

A recipe can work with different preprocessors at the same time.

The setting additional_datasets can be used to add a different dataset.

Variable groups are useful for defining different settings for different variables.

previous episode

ESMValTool Tutorial

next episode

Writing your own recipe

Overview

Introduction

Drawing up a plan

Answer

Building a recipe from scratch

Pro tip: config-references.yml

Adding a dataset entry

Filling in the dataset keys

Answers

Adding the preprocessor section

Defining the preprocessor

Solution

Completing the diagnostics section

Fill in the blanks

Solution

Bonus exercises

Specific location

Solution

Different periods

Solution

Different preprocessors

Solution

Additional datasets

Solution

Key Points

previous episode

next episode

key	file 1	file 2
project	CMIP6	CMIP5
short name	tas	tas
CMIP table	Amon	Amon
dataset	BCC-ESM1	CanESM2
experiment	historical	historical
ensemble	r1i1p1f1	r1i1p1
grid	gn (native grid)	N/A
start year	1850	1850
end year	2014	2005